On the Problem of Multiple Matching
by I.L. BATTIN
Drew University
Introduction.
The problem of determining the distribution of the number of "hits" or "matchings" under random matching of two decks of cards has received attention from a number of authors within the last few years. In 1984 Chapman [2] considered pairings between two series of t elements each, and later [3] generalized the problem to series of u and t (R u) elements respectively. In the same paper he also considered the distribution of the mean number of correct matchings resulting from n independent trials, and gave a method, and tables, for determining the significance of any obtained mean. In 1937 Bartlett [1] considered matchings of two decks of cards, using a number of interesting moment generating functions.
| |
In 1937 Huntington [12, 13] gave tables of probabilities for matchings between decks with the compositions (55), (44), and (33), where (st) denotes a deck consisting of s of each of t kinds of cards. More generally (s1s2…st) denotes si cards of the first kind, s2 of the second, etc. Sterne [16] has given the first four moments of the frequency distribution for the (55) case and has fitted a Pearson Type I distribution function to the distribution. Sterne obtained his results by considering the probabilities in a 5 X 5 contingency table. He also considered the 4 X 4 and 3 X 3 cases. In 1938 Greville [7] gave a table of the exact probabilities for matchings between two decks of compositions (55). Greenwood [4] obtained the variance of the distribution of hits for matchings between two decks having the respective compositions (st) and (s1s2…st) with si s1 +s2 +… st = st = n, and where it is not necessary that all the s's should be different from zero. Earlier Wilks [19] had considered the same problem for t = 5 and n = 25.
In a very interesting paper Olds
[15] in 1938 used permanents to express a moment generating function suitable
for the problem in question. He obtained factorial moments and the first four
ordinary moments about the mean, first for two decks with composition (42), and then for two decks of composition
(st) . In
1938 Stevens [17] considered a contingency table in connection with matchings
between two sets of n objects
each, and gave the means, variances, and covariances of the single cell entries
and various sub-totals of the cell entries. Stevens [18] also gave a treatment
of the problem of matchings between two decks which was based on elementary
considerations. In 1940 Greenwood [6] gave the first four moments of the distribution
of hits between two decks of any composition whatever, generalizing the problem
which had been treated earlier by Olds [15]. Finally in 1941, Greville [8]
gave the exact distribution of hits for matchings between two decks of arbitrary
composition. He also considered the problem from the standpoint of a contingency
table, as had been done earlier by Stevens.
In 1939 Kullback [14] considered matchings between two sequences obtained by drawing at random a single element in turn from each of n urns Ui containing elements of r types Ej in the respective proportions pij. He showed that if the process of drawing were indefinitely repeated the distribution of hits would be that of a Poisson series.
The work which has been done thus far applies to the problem of matching two decks of cards. In the present paper a method is developed for obtaining the moments of the distribution of hits for matchings between three or more decks of cards of arbitrary composition.
2. Matchings between two Decks of cards.
In the present paper it will be
convenient to take as the point of departure the method used by Wilks [19]
in his treatment of the problem of hits occurring under random matching of
two decks of 25 cards each, namely a target deck with composition (55) and
a matching deck with composition ![]() . He showed that
. He showed that

where, 
is a suitable generating function
for obtaining the moments of the distribution.
In fact, if we define an operator ![]() as
as
![]()
where
![]() ,
and if h denotes the number of hits, then for r = 1, 2, ...
, 5,
,
and if h denotes the number of hits, then for r = 1, 2, ...
, 5,
P(h = r) = coefficient of ![]() in
in
![]()
And it is readily seen that

Wilks' ![]() function
involves a particular order for the target deck. If we are to generalize and
obtain moments for matchings between more than two decks, it is obvious that
we must devise a procedure which will, in the case of two decks, be perfectly
symmetrical and not require that one deck be given a preferred status. In
the case of two decks this is readily accomplished by the use of Kronecker
deltas, and in the case of three or more decks by the use of obvious generalizations
of these deltas.
function
involves a particular order for the target deck. If we are to generalize and
obtain moments for matchings between more than two decks, it is obvious that
we must devise a procedure which will, in the case of two decks, be perfectly
symmetrical and not require that one deck be given a preferred status. In
the case of two decks this is readily accomplished by the use of Kronecker
deltas, and in the case of three or more decks by the use of obvious generalizations
of these deltas.
For two decks of 25 cards each with compositions (55) we need only let

where ![]() .
Then, if
.
Then, if

it readily follows that

More
generally, for two decks of
n cards each, the cards being of k types, and the decks having compositions ![]() respectively,
we let
respectively,
we let
![]() .
.
The
factors of 0 are in one-to-one correspondence with the n events of dealing a card from each of the two decks. The values
which can be assumed by the subscripts i and j are in one-to-one correspondence with the k types of cards. The symbol xi corresponds to the first deck, yi to the second, the subscripts i and j corresponding to the different types of cards in each deck. The
expansion of ![]() consists
of all products which can be formed by choosing one and only one pair
consists
of all products which can be formed by choosing one and only one pair
![]() from
each factor of
from
each factor of ![]() as
a factor of the product. In forming any term of
as
a factor of the product. In forming any term of ![]() , choosing
, choosing
![]() . from any
factor of
. from any
factor of ![]() corresponds to dealing a card of type
corresponds to dealing a card of type ![]() from both decks, and introduces
from both decks, and introduces ![]() into the coefficient of the term. Choosing
into the coefficient of the term. Choosing ![]() from
any factor corresponds to dealing a card of type
from
any factor corresponds to dealing a card of type ![]() from
the first deck,
from
the first deck, ![]() from
the second. If
from
the second. If ![]() , then, since
, then, since
![]()
![]() is not introduced into the coefficient. Therefore in the coefficient
of any term of
is not introduced into the coefficient. Therefore in the coefficient
of any term of ![]() ,
, ![]() will be raised to a power, say s, which is equal to the number of factors of
will be raised to a power, say s, which is equal to the number of factors of ![]() from which pairs
from which pairs ![]() . have been
chosen.
. have been
chosen.
The total number of ways in which the term
![]()
can arise is equal to the number
of ways in which two decks of types ![]() respectively
can be dealt, {where
respectively
can be dealt, {where ![]() and similarly for
and similarly for ![]() }. But
this is given by
}. But
this is given by

The coefficient of ![]() in
in
 is
the total number of ways in which the term
is
the total number of ways in which the term ![]()
can
be formed subject to the restriction that pairs ![]() are
chosen from s of the factors of
are
chosen from s of the factors of ![]() . But this
is precisely the number of ways in which the two decks can be dealt so that
there will be s hits. Hence if, as above, h is the number of hits, the probability that h
= s, assuming all permutations in each deck to be equally likely, is
given by
. But this
is precisely the number of ways in which the two decks can be dealt so that
there will be s hits. Hence if, as above, h is the number of hits, the probability that h
= s, assuming all permutations in each deck to be equally likely, is
given by

Since this is true for all values of s it follows that

Since

we have at once


It is an equally straightforward matter to show that

and that
Evidently any of the ![]() and
and ![]() may be zero, provided only that
may be zero, provided only that 
The case of two decks with unequal numbers of cards m and n,(m < n), is readily handled by substituting for the smaller deck one obtained by adding n-m "blank" cards - that is, cards of any type not already appearing in either deck, as indicated by Greville [8], who however obtained his results by considering a preferred order for one of the decks.
EXAMPLE 1. In the case of the decks treated by Wilks [19], n = 25, k = 5, n1i = n2j = 5.
Hence from ( ![]()
and from 
EXAMPLE 2.
Suppose we have two decks as shown by the
scheme
Type of cards |
Total of all types |
|||||
| 1 |
2 |
3 |
4 |
5 |
||
N° in deck A |
5 |
7 |
8 |
0 |
0 |
20 |
| N° in deck B |
0 |
3 |
4 |
6 |
2 |
15 |
Here deck B has five fewer cards
than deck A. Hence we must presume that there are six types of cards in all,
and that the decks have the respective distributions (578000) and (034625).
We then have at once
![]()
And

- 3. Matchings between three
decks.
Let the three decks be of types ![]() respectively,
with
respectively,
with  , and consider
the function
, and consider
the function
where
![]()
and the other deltas are the usual Kronecker symbols.
Each factor of ![]() corresponds
to one deal from each of the three decks. The symbols x, y, and z correspond respectively to cards in the first,
second, and third decks. The subscripts
i, j, k, = 1, 2, …q correspond to the types of cards - there
being q
distinct types.
corresponds
to one deal from each of the three decks. The symbols x, y, and z correspond respectively to cards in the first,
second, and third decks. The subscripts
i, j, k, = 1, 2, …q correspond to the types of cards - there
being q
distinct types.
Choosing ![]() from a factor
of
from a factor
of ![]() corresponds
to a deal in which a card of type a is dealt from all three decks, and introduces
corresponds
to a deal in which a card of type a is dealt from all three decks, and introduces
 into the coefficient
of the corresponding term in the expansion of
into the coefficient
of the corresponding term in the expansion of ![]() . Similarly, choosing
. Similarly, choosing
![]() , corresponds
to a hit between the first and second decks, and introduces
, corresponds
to a hit between the first and second decks, and introduces  into the coefficient.
Similarly choosing
into the coefficient.
Similarly choosing ![]() introduces
introduces
 ;
;
![]() introduces
introduces  . Choosing
. Choosing
 corresponds to a deal with no hits, and introduces
no powers of e into
the coefficient, since all the d's are zero.
corresponds to a deal with no hits, and introduces
no powers of e into
the coefficient, since all the d's are zero.
Let  be
defined by :
be
defined by :
![]()
Then the coefficient of
 is
the number of ways in which the cards can be dealt so as to yield precisely
h123 triples, or hits between all three decks.
Similarly the coefficient of
is
the number of ways in which the cards can be dealt so as to yield precisely
h123 triples, or hits between all three decks.
Similarly the coefficient of 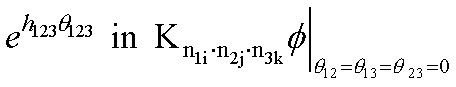 is
the number of ways in which the cards can be dealt so as to yield precisely
h12 hits between the first and second decks, with corresponding results for
the first and third (h13) and second and third (h23) decks.
is
the number of ways in which the cards can be dealt so as to yield precisely
h12 hits between the first and second decks, with corresponding results for
the first and third (h13) and second and third (h23) decks.
By the same reasoning as before then, we have


with similar results for h13 and h23 . And it is a straightforward matter to show that






with corresponding results for other moments. It is understood each summation
index takes values from 1 to q.
As before, if the decks do not all have the same total number of cards it is merely necessary to introduce one or more sets of "blank" cards. Thus we would replace decks with the compositions (57800), (03462), (00335) by hypothetical decks (5780000 ), (0346250), (0033509) and proceed as before.
EXAMPLE 3. For three decks of 25 cards,
consisting of five of each of five kinds we have n = 25, ![]() .
.
Hence






with similar results for 
 and
and

4.
Generalization to any number of decks.
If the moments of the distribution of hits --doubles,
triples, quadruples, . . .-- in matching any number of decks is desired, these
can be obtained by using an obvious generalization of . Thus for four decks we would define
![]() not
all equal, and use
not
all equal, and use

However, it is evident that as the number of decks is increased the summations
involved and the manipulation of the (generalized) K
operators rapidly become complicated.
5. Application of our
moment-generating technique to two-way contingency tables.
The moment-generating technique
which we have discussed has wider applications than merely to matching problems.
As an example of considerable interest we shall consider the contingency problem.
Consider the array
and also the function
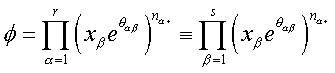
If i and j
are particular values of a and b respectively, then to the i-th
row of the array corresponds the product  , consisting
of
, consisting
of ![]() identical
factors
identical
factors ![]() , one such
factor corresponding to each of the
, one such
factor corresponding to each of the ![]() elements in the row. To the
j-th column of the array corresponds the xj which appears in each of the factors of
elements in the row. To the
j-th column of the array corresponds the xj which appears in each of the factors of
![]() . To the
ij-th cell of the array corresponds
. To the
ij-th cell of the array corresponds ![]() which appears
only in the factors
which appears
only in the factors 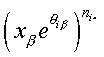 , and
in each of these only as the coefficient of xj
, and
in each of these only as the coefficient of xj
The expansion of ![]() consists
of all products which can be formed by taking as factors one and only one
element
consists
of all products which can be formed by taking as factors one and only one
element  ,'
(not summed) from each factor of
,'
(not summed) from each factor of ![]() .
But taking
.
But taking  from
one of the factors
from
one of the factors  of
of
![]() corresponds
exactly to putting an element in the ij-th
cell of a lattice such as . Hence every term in the expansion of
corresponds
exactly to putting an element in the ij-th
cell of a lattice such as . Hence every term in the expansion of
![]() corresponds
to a particular distribution in such a lattice. Moreover, all terms of
corresponds
to a particular distribution in such a lattice. Moreover, all terms of
![]() correspond
to distributions in which the row totals are
correspond
to distributions in which the row totals are  ,
for we must take ni. elements from the product
,
for we must take ni. elements from the product  Further,
those terms in which the
Further,
those terms in which the ![]() appear
in the particular product
appear
in the particular product  correspond
to distributions in which the column totals are
correspond
to distributions in which the column totals are ![]() , since choosing
, since choosing
![]() elements
elements
 corresponds
to putting
corresponds
to putting ![]() elements
in the j-th
column and some row of the lattice.
elements
in the j-th
column and some row of the lattice.
Expanding ![]() we
obtain
we
obtain
where the summation is over all partitions
![]()
It is clear that since every set of values of the ![]() subject
to the partition restrictions
subject
to the partition restrictions ![]() corresponds
to a particular distribution of n
elements in the lattice , every particular product
corresponds
to a particular distribution of n
elements in the lattice , every particular product  corresponds
to such a distribution, and represents the number of ways in which it can
arise. Further, the total coefficient displayed , namely
corresponds
to such a distribution, and represents the number of ways in which it can
arise. Further, the total coefficient displayed , namely  ,
represents the total number of ways in which distributions with row totals
,
represents the total number of ways in which distributions with row totals
![]() and
column totals
and
column totals ![]() can
arise. Setting all the
can
arise. Setting all the ![]() we
readily find
we
readily find

Hence the probability of any particular distribution ![]() with
fixed row totals
with
fixed row totals ![]() and
fixed column totals
and
fixed column totals ![]() is
:
is
:

Moments of the nij
Consider now the result of differentiating ![]() with respect
to a particular
with respect
to a particular ![]() . We obtain
. We obtain

where ![]() denotes summation
over indices such that
denotes summation
over indices such that ![]() . Now
. Now
![]() , but also
nij can never be less than
, but also
nij can never be less than
![]() . For
. For
![]() . Since the
maximum value of
. Since the
maximum value of ![]() the
maximum value of
the
maximum value of ![]() .
.
Hence
![]()
Therefore
![]()
Accordingly, combining all the terms of in which nij has a particular value, g, we have

where S* denotes summation and P* multiplication with nij = g.
Since  is
precisely the number of distributions
is
precisely the number of distributions  for which nij = g, it follows that
for which nij = g, it follows that

Similarly it follows that


where we may have (i = k)
or (i ≠ k),
and (j =
l))or (j ≠ l).
By straightforward differentiation and reduction we find that for the array
with given marginal totals ![]()








Moments of the distribution of Chi Square.
For the array :

Hence, using the above results
we can, theoretically, find all the moments of the exact distribution Of
![]() . It is not
difficult to show that
. It is not
difficult to show that

The value of ![]() and the variance
of
and the variance
of ![]() . were found
by straightforward application of our methods and the results agreed with
those given by Haldane [10].
. were found
by straightforward application of our methods and the results agreed with
those given by Haldane [10].
The writer is indebted to Professor Wilks for helpful criticisms and suggestions.
REFERENCES
[1] M. S. BARTLETT, "Properties of sufficiency and statistical tests," Proc. Roy. Soc., A, Vol. 160 (1937), pp. 268-282.
[2] DWIGHT CHAPMAN, "The statistics of the method of correct matchings," Amer. Jour. Psych., Vol. 46 (1934), pp. 287-298.
[3] DWIGHT CHAPMAN, "The generalized problem of correct matchings," Annals of Math. Stat., Vol. 6 (1935), pp. 85-95.
[4] J. A. GREENWOOD, "Variance of a general matching problem," Annals of Math. Stal., Vol. 9 (1938), pp. 56-59.
[5] J. A. GREENWOOD, "Variance of the ESP call series," Jour. of Parapsychology, Vol. 2 (1938), pp. 60-64.
[7] T. N. E. GREVILLE, "Exact probabilities for the matching hypothesis," Jour. of Parapsychology, Vol. 2 (1938), pp. 55-59.
[8] T. N. E. GREVILLE, "The frequency distribution of a general matching problem," Annals of Math. Stat., Vol. 12 (1941), pp. 350-354.
[9] J. B. S. HALDANE, "The mean and variance of Chi square, when used as a test of homogeneity, when expectations are small," Biometrika, Vol . 31 (1940).
[10] J. B. S. HALDANE, "The first six moments of Chi-square for an n-fold table with n degrees of freedom when some expectations are small," Biometrika, Vol. 29 (1939), p. 389.
[11] J. B. S. HALDANE, "The exact value of the moments of the distribution of chi-square, used as a test of goodness of fit, when the expectations are small," Biometrika, Vol. 29 (1939), p. 133.
[12] E. V. HUNTINGTON, "A rating table for card matching experiments," Jour. of Parapsychology, Vol. 4 (1937), pp. 292-294.
[13] E. V. HUNTINGTON, "Exact probabilities in certain card-matching problems," Science, Vol. 86 (1937), pp. 499-500.
[14] SOLOMON KULLBACK, "Note on a matching problem," Annals of Math. Stat., Vol. 10 (1939), pp. 77-80.
[15] E. G. OLDS, "A moment-generating function which is useful in solving certain matching problems," Bull. Amer. Math. Soc., Vol. 44 (1938), pp. 407-413.
[16] T. E. STERNE,, "The solution of a problem in probability," Science, Vol. 86, (1937) pp. 500-501.
[17] W. L. STEVENS, "Distribution of entries in a contingency table," Annals of Eugenics, Vol. 8 (1938), pp. 238-244.
[18] W. L. STEVENS, "Tests of significance for extra sensory perception data," Psychological Review, Vol. 46 (1938), pp. 142-150.
[19] S. S. WILKS, "Statistical aspects of experiments in telepathy," a lecture delivered to the Galois Institute of Mathematics, Long Island University, December 4, 1937.











