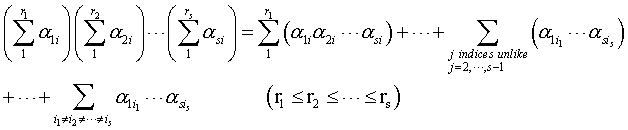THE FIRST FOUR MOMENTS OF A GENERAL MATCHING PROBLEM

By JOSEPH A. GREENWOOD, Duke University, U.S.A.

(Annals of Eugenics, 1940, 10)

The first two moments of the case under consideration were obtained by Stevens (1938, 939). Stevens noted that his method was extensible to obtaining the higher moments. This paper supplies the actual values of the first four moments as obtained from a somewhat different viewpoint [1] .

The situation is the random matching of two decks of cards of numbers a_i and b_i , respectively, of the i-th symbol, i = 1, 2, ..., t. If one deck has more cards than the other, it assumed that enough blank cards have been added to the deficient deck to equalize the totals with the blank standing for a new symbol. Thus the matching of two arbitrary decks is possible.

Let , and let the a deck be arranged in the order of symbols whose numb are a₁, a₂, ..., a_t. When the b deck is shuffled and matched card for card with the a deck certain positions will be hits and the rest misses. Associate the numbers 1 and 0, respectively, with these positions. Basing the notation on the fixed deck, X_ij is a variable taking on the value 1 if a hit occurs at the jth card of the ith symbol, otherwise 0. Then , is the score of a given matching. We shall use the symbol p( ) to denote the expected value of the quantity in the brackets, so that the mean of X,

                                                  

exactly as Stevens obtained it.

For economy of notation define

                          

and, for example, SAB to mean , where [2]

                                                     

                                  

                                                 

                                           

As an example of the counting process involved in the summations, note that there are ordered pairs , all having the same expectation. Thus

                                                     

                                       

In order to reduce the second expression in the brace and the more complicated ones to be encountered later on, the following formula is included :

                                                                                          

As a special case of  . Making the above substitutions in  one obtains

                                                                                                                                                                                

which is Stevens’s formula.

Proceeding analogously for the third moment, the major steps will be listed.

The last three terms are the only new ones to be evaluated since, for example,

                                                

By simple counting as in the  case one obtains

Eliminating the inequality summations by and substituting in

                                      

there results :

                                                                                                                                       

The same procedure is followed to obtain :

Again, noting that , for example, and evaluating the new terms in X⁴ one finds

Applying to the inequality summations and substituting in

there results

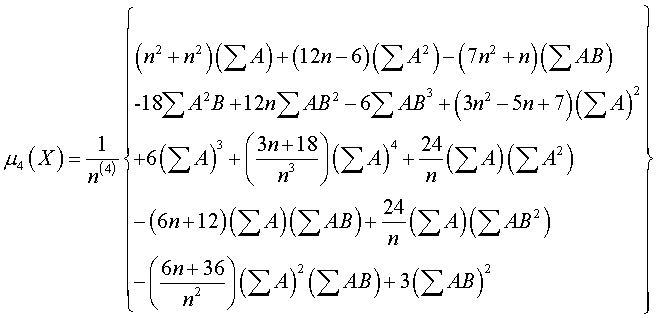
Olds (1938) gave the first four moments of the case wherein . The sign S  then merely means multiplication by n/s. Also A = s²

, B = 2s. With these substitutions the above four moments reduced to the expressions given by Olds.

A computing arrangement is the scheme,

An example work out for

gave

References

W.L. Stevens (1938), Distribution of entries in a contingency table with fixed marginal totals, Ann. Eugen., Lond., 8, 238.

W.L. Stevens (1939), Tests of significance for extra sensory perception data, Psychol. Rev.46, 2, March.

E.G. Olds(1938), A moment-generating function which is useful in solving certain matching problems, Bull. Amer. Math. Soc., June.