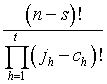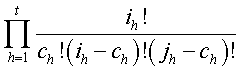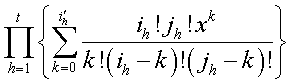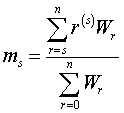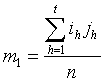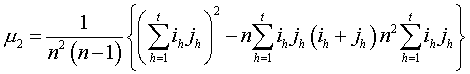THE FREQUENCY DISTRIBUTION OF A GENERAL MATCHING PROBLEM

By T. N. E. GREVILLE

Bureau of the Census

(Annals of mathematical statistics, 1941, 12, 350-354)

1. Introduction.

This paper considers the matching of two decks of cards of arbitrary composition, and the complete frequency distribution of correct matchings is obtained, thus solving a problem proposed by Stevens. It is also shown that the results can be interpreted in terms of a contingency table.
Generalizing a problem considered by Greenwood (1938) let us consider the matching of two decks of cards consisting of t distinct kinds, all the cards of each kind being identical.

The first or "call" deck will be composed of i₁ cards of the first kind, i₂ of the second, etc., such that

and the second or "target" deck will contain j₁ cards of the first kind, j₂ of the second, etc., such that

Any of the i's or j's may be zero. It is desired to calculate, for a given arrangement of the "call" deck, the number of possible arrangements of the "target" deck which will produce exactly r matchings between them (r = 0, 1, 2, .. . , n). It is clear that these frequencies are independent of the arrangement of the call deck. For convenience the call deck may be thought of as arranged so that all the cards of the first kind come first, followed by all those of the second kind, and so on.

2. Formulae for the frequencies.

Let us consider the number of arrangements of the target deck which will match the cards in the k₁th, k₂th, … , k_sth positions in the call deck, regardless of whether or not matchings occur elsewhere. Let the cards in these s positions in the call deck consist of c₁ of the first kind, c₂ of the second, etc. Then:

The number of such arrangements of the target deck is

(1)

For fixed values of the c's, the s specified positions may be selected in

(2)

ways.

Consider now the expression

(3)

obtained by summing the product of (1) and (2) over all sets of values of the numbers satisfying the conditions .

Let W, denote the number of arrangements of the target deck which result in exactly s matchings. Then it is evident that V, exceeds W, since the former includes those arrangements which give more than s matchings, and these, moreover, are counted more than once. Consider an arrangement which produces it matchings, where u > s. Such an arrangement will be counted once in V for every set of s matchings which can be selected from the total of u- that is times. In other words,

It has been shown (Geiringer, 1938) that the solution of these equations is

(4)

3. Computation of the frequencies.

Equations (3) and (4) apparently give the solution of the problem, but in practice the labor of carrying out the summation indicated in (3) would often be very great. However,(3) may be rewritten in the form

(5)

where

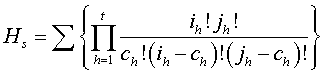
It will be seen that H_s is the coefficient of in the product

(6)

where denotes the smaller of i_h and j_h . The factor was included in H_s in order to make the coefficient in the polynomials of (6) always integers. Equation (4) may now be written in the form

(7)

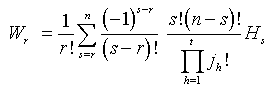
a form which lends itself to actual computation.

4. Factorial moments.

The factorial moments of the frequency distribution of the number of matchings are easy to compute. Let m_s. denote the sth factorial moment, so that

(8)

Substituting from (4)

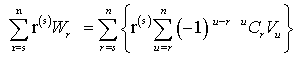
Reversing the order of summation and simplifying,

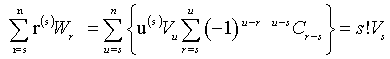
Hence,

(9)

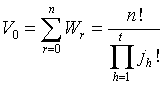
and from (5) and (8),

(10)

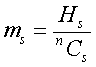
5. Mean and variance.

From (6)

(11)

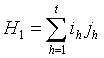
and

(12)

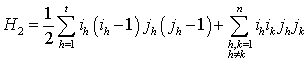
Hence the mean number of matchings is

(13)

The variance m₂ is

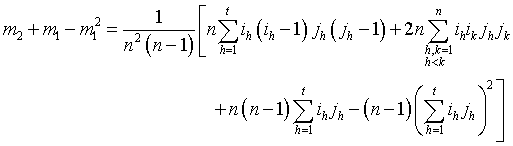
or

(14)

In the special case these formulae become

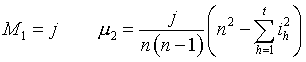
These formulae have previously been given by Stevens, and those for the special case also by Greenwood. The maximal conditions for the variance, given by Greenwood for this particular case, apparently can not be put in a simple form for the general case.

6. Unequal decks.

Suppose the call deck contains m cards, m < n, and is to be matched with m cards selected from the target deck. It can be assumed without loss of generality that the first m cards in any arrangement of the target deck are the ones to be used. The formulae of this paper can be applied to this more general problem by the expedient of imagining n - m blank cards to be added at the end of the call deck and regarding these as an additional kind. It is thus apparent that formulae (13) and (14) apply without modification to this altered situation.

7. Application to contingency table.

Stevens has considered the distribution of entries in a contingency table with fixed marginal totals, and has pointed out that the problem of matching two decks of cards may be dealt with from that standpoint. A contingency table classifies data into n columns and m rows, and we may consider the row as indicating the kind of card which occupies a given position in the call deck, the columns having the same function with respect to the target deck. Stevens defines a quantity c as the sum of entries in a prescribed set of cells, subject to the condition that no two cells of the set are in the same row or column, and mentions as unsolved the problem of the exact sampling distribution of c.
We now have at our disposal the machinery for solving this problem. Following Stevens's notation, let denote the fixed row totals and . the fixed column totals, while denotes the frequency of the cell in the rth row and the sth column. Then, let where does not exceed either m or n. Imagine two decks of N cards , the first containing a₁ cards of one kind, a₂ of another, etc., and the second containing b₁ cards of one kind, b₂ of another, etc. Moreover, let the r_hth kind in the first deck and the s_hth kind in the second deck be the same kind (h = 1, 2, - … , l), the other kinds being all different. Evidently c is the number of matchings between the two decks. Hence, the methods of this paper can be used to obtain the distribution of c. The formulae we have obtained agree with those for the expected value and variance of c given by Stevens.